PA3FWM,是大名鼎鼎 http://websdr.ewi.utwente.nl:8901/ 的制造者,最近看到他个人网站,上面有很多好东西,特此转载,以供学习!
https://www.pa3fwm.nl/technotes/tn34-gilbert-cell-mixer.html 通过此文章,我了解到我们喜爱的NE602混频器已经停产,在此向此电路的设计人员致敬。
吉尔伯特单元混频器
Pieter-Tjerk de Boer,PA3FWM pa3fwm@amsat.org
(这是我为荷兰业余无线电杂志Electron 撰写的文章的一部分的改编版本,2023 年 5 月。)
NE602混频器在许多业余电路中广为人知,今年将与其兄弟 NE612、SA602、SA612 一起停产。因此,是时候寻找替代方案并了解此类芯片的工作原理了。
混合:加法还是乘法?
根据上下文,“混合”两个模拟信号(如电压)可能意味着将它们相加或相乘。例如,在音频信号的情况下,混合意味着相加;想象一下录音室中的混音控制台,或者计算机中的“混音器”设置。添加电压后,不会出现新的频率。然而,在无线电技术中,混频器是一种产生和频和差频的电路。为了实现这一点,电压必须倍增。执行此操作的一个非常常见的电路被称为“吉尔伯特单元”,尽管这并不公平。
吉尔伯特单元的原理
该图(从数据表复制)显示了NE602的内部电路,这也是吉尔伯特单元的教科书示例。
首先考虑晶体管 T1 和 T2。它们的发射极相连,因此它们的发射极电流都通过共发射极电阻流至地。换句话说,该发射极电流由两个晶体管在其集电极之间分配。如果两个基极(可用作芯片的引脚 1 和 2)电压相同,则电流将平均分配。如果引脚 1 相对于引脚 2 为正,则 T1 导通较多,T2 导通较少,因此它们的联合发射极电流的较大部分将发送至 T3 和 T4,而不是发送至 T5 和 T6;当然,如果引脚 1 相对于引脚 2 为负,则反之亦然。
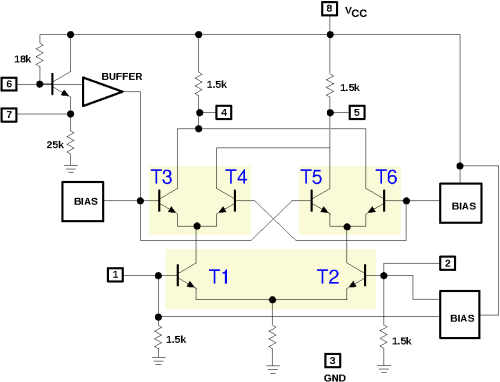
此过程在 T3 和 T4 以及 T5 和 T6 重复。它们也将根据基极电压分配联合发射极电流。如果T3的基极相对于T4的基极为正,则更多的电流将流向左集电极电阻;否则更多到正确的集电极电阻。T5 和 T6 的做法相同,但方向相反,因为它们的集电极与 T3 和 T4 的集电极交叉连接。
让我们将 T1 和 T2 基极之间的电压视为一个输入(芯片的引脚 1 和 2),将 T3 和 T4(以及 T5 和 T6)基极之间的电压视为另一输入(引脚 6)。然后我们看到,如果两个输入均为正,则大部分电流将流向左侧集电极电阻(通过 T1 和 T3);如果两个输入均为负(但通过 T2 和 T6),也会发生这种情况。但如果一个输入为负,另一个输入为正,则大部分电流将流向右侧集电极电阻(通过 T1 和 T4,或 T2 和 T5)。电路的输出是引脚4和5之间的电压;这是正值还是负值取决于哪个集电极电流最大。结果:加和加给出加;加号和减号给出减号;等等:这是乘法! 如果(至少)一个输入为 0,则无论另一个输入如何,两个集电极电阻都会获得相等的电流(得益于 T5 和 T6 与 T3 和 T4 交叉连接的方式);这也适合乘法。不幸的是,这个乘法并不是很好的线性,我们稍后会看到。
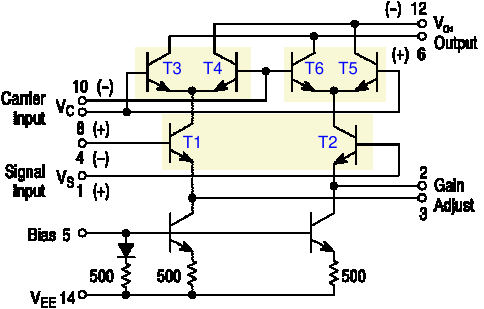
下图显示了另一个混频器芯片 MC1496。在这里我们再次看到六个晶体管的相同组合。但该芯片比NE602更基础:用户需要连接一些电阻用于直流偏置,并且T3...T6前面没有前置放大器(在NE602中也可以用作振荡器)。另一方面,MC1496没有简单的发射极电阻,而是有两个电流源(底部的两个晶体管),用户可以在T1和T2的发射极之间连接一个电阻。
长尾对
在吉尔伯特单元混频器中,我们看到了同一子电路的三个副本,由两个发射极相连的晶体管组成。该子电路被称为“长尾对”,请参见下图 (a)。让我们精确计算一下它的作用。
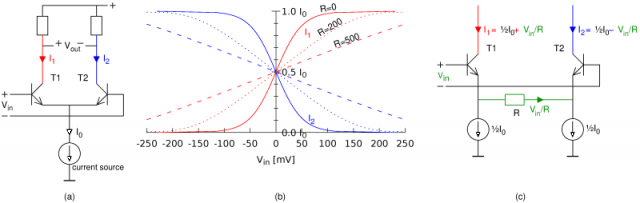
对于一般晶体管,集电极电流与 exp( V BE /25 mV) 成正比。实际上,这意味着 BE 电压每增加 17 mV,集电极电流就会加倍。因此,如果输入电压(施加在两个基极之间)为 17 mV,则左侧晶体管需要消耗右侧晶体管两倍的集电极电流。它们的总数仍然是I 0,由电流源强制。因此,左侧晶体管获得 ⅔ I 0,而右侧晶体管获得 ⅓ I 0。类似地,在输入电压为 34 mV 时,晶体管获得I 0的 80% 和 20% 。这如图 (b) 中的实线所示:显然,输入电压和两个输出电流之间的关系不是线性的。这也意味着基于长尾对如何分配电流的吉尔伯特电池不能线性工作。
图 (c) 显示了长尾对的一种变体,发射极之间有一个电阻器R。只要V in为 0,就没有什么区别:电阻两端的电压为 0 伏,因此没有电流流过它,并且两个集电极电流又都是 ½ I 0。如果V in不为零,并且我们(为简单起见)假设两个 BE 电压都是恒定的(众所周知的 0.6 伏),则完整的V in位于电阻器两端。由于电流源坚持每个电流源汲取 ½ I 0,因此电流V in / R必须流过晶体管:其中一个晶体管将具有 ½ I 0 + V in / R ,另一个则具有 ½ I 0 - V in / R。差异恰好是V in / R。
如前所述,这是在 BE 电压相等的假设下进行的。实际上,它们会随着集电极电流的变化而发生一些变化,因此这种关系会有点非线性。见图(b)中的虚线:R越大,线性越好,但增益也越小。
现在,我们了解了连接在 MC1496 引脚 2 和 3 之间的电阻器的功能:它允许用户在更高线性度或更高增益之间进行选择。另一方面,NE602 采用硬连线以获得最大增益,事实上,该芯片因不具有良好的互调性能(线性度)而闻名。对于这两个芯片,驱动 T3...T6 的第二个输入是非线性的;对于其线性度,发射极电阻没有帮助。
吉尔伯特乘法器
尽管上面讨论的混频器电路被称为“吉尔伯特单元”,但它是由 Howard E. Jones 发明的 [3]。巴里吉尔伯特是一种不同但相似的电路的发明者。AD534 是最早采用该电路的芯片之一,此处显示了其内部原理图。T1...T6周围的电路看起来与之前的电路非常相似,但本质的区别是增加了T7和T8。它们确保混频器的第二个输入(通过 T9 和 T10)也是线性的。

为了理解吉尔伯特是如何实现这一目标的,我们首先要研究模拟芯片技术的另一个子电路,即所谓的“电流镜”,见图(a)。该电路包含两个晶体管;电流I 1是输入,电流I 2是输出。左侧晶体管基极上的电压将稳定下来,使其集电极电流为I 1(我们暂时忽略基极电流)。由于基极-发射极电压和集电极电流之间存在指数关系,因此该基极电压将与输入电流的对数成正比。该相同的BE 电压也是右侧晶体管的 BE 电压,其集电极电流与此呈指数关系。最终结果是I 2线性依赖于I 1,尽管晶体管本身是非线性的!
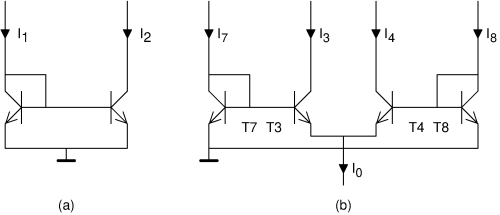
受到当时(1968 年)已广为人知的电流镜的启发,吉尔伯特提出了(b)所示的电路。这类似于两个电流镜 T7+T3 和 T5+T8,只不过并非所有发射极都连接在一起。基极-发射极-结一起形成一个环路,仔细观察,可以看到T7的BE电压减去T3的BE电压,必须等于T8的BE电压减去T4的BE电压。由于每个晶体管的BE电压和集电极电流之间存在指数关系,因此可以得出I 7 / I 3 = I 8 / I 4。换句话说,I 7 : I 8 = I 3 : I 4。此外,我们仍然有 I 3 + I 4 = I 0 (再次忽略基极电流)。现在,如果I 0来自电流源(因此恒定),并且我们将I 7和I 8视为输入信号,则该电路将以与I 7与I 相同的比例将I 0除以I 3和I 4 8 . 写成公式:I 3 = I 0 · I 7 / ( I 7 + I 8 )。如果I 7 + I 8保持不变,那么这是一个非常简洁的乘法。但它只适用于正数(因为晶体管不允许负电流)。
为了也处理负数,我们需要更多,这就是我们如何得到前面所示的 AD534 原理图。其中 T3...T8 形成吉尔伯特的实际乘数。T1和T2与发射极电阻形成长尾对,以获得良好的线性度,T9和T10也是如此。它们将输入电压V x和V y转换为差分电流;差分是指两个电流之间的差值就是实际信号。因此,输入电压V x决定了T1和T2集电极电流之间的差值。接下来,就像第一幅图中一样,T1的集电极电流被分配给T3和T4,T2的集电极电流被分配给T5和T6;但由于 T7 和 T8 的存在,这种划分现在精确地与 T9 和 T10 的集电极电流之比,从而与输入电压V y之比。(请注意,与图 (b) 相比,T7 和 T8 是“颠倒的”,但它们仍然具有相同的功能。)因此,对于正输入电压V x和负输入电压V y ,我们获得了良好的线性乘法。
为了完整起见:AD534 电路底部的四个未编号的晶体管再次是电流源,并且在运算放大器 A1 周围构造了一个放大器,用于将 T3...T6 的差分输出电流转换为非差分输出电压。
琼斯 VS 吉尔伯特
现在我们有了第一幅图(NE602)中的电路,它是由琼斯发明的,但被称为“吉尔伯特单元”,以及第四幅图(AD534)中吉尔伯特发明的电路,但它实际上并没有任何意义。姓名。电路看起来很相似,所以混乱是可以理解的。吉尔伯特似乎在不知道琼斯电路的情况下发明了他的电路,并且他试图纠正命名;但一旦错误的名字被普遍使用,就很难改变。
在混频器应用(如 MC1496 和 NE602)中,人们几乎总是会看到琼斯电路。吉尔伯特电路提供的唯一优点是它对于第二个输入信号也是线性的。对于通常不需要的搅拌机。第二个输入信号通常用于本地振荡器,如果它有点失真,就会出现谐波,这通常不是什么大问题。事实上,混频通常是有意使用方波信号来完成的。例如,在二极管环形混频器中,二极管充当由振荡器信号打开和关闭的开关。这也可以在吉尔伯特单元中完成(我们将继续使用琼斯设计的名称):如果在 T3/T5 和 T4/T6 的基极之间施加大交流电压,这些晶体管将充当开关,发送 T1 和T2的集电极电流完全流向一个或另一个集电极电阻.
关于巴里·吉尔伯特的更多信息
据我所知,除了他的混频器电路之外,在电气工程领域,人们对琼斯的了解不多。相比之下,吉尔伯特(1937-2020)有着丰富的职业生涯,他在[5]中回顾了这一点。在他年轻的时候,他就已经开始制造电视机了。在大盾工作时,他对示波器技术着迷,这使他在泰克找到了一份工作,在那里他还发明了乘法器电路。后来他在 Analog Devices 担任了很长时间的芯片设计师。
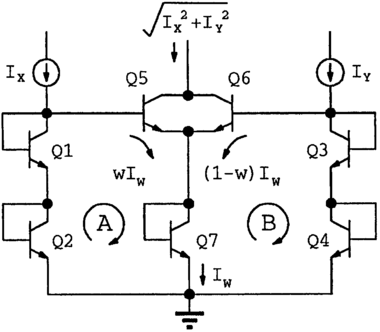
在图(b)中,我们看到他利用晶体管中电流和电压之间的指数关系来很好地线性地倍增电流。(顺便说一句,这类似于计算尺通过添加距离来执行乘法的方式。)后来他概括了这个想法,并将其称为“跨线性原理”。它可用于设计对电流和电压执行数学运算的各种电路。例如,此处显示的电路“计算”毕达哥拉斯公式 √( x 2 + y 2 )。
他最明显的贡献,至少从字面意义上来说,是泰克 7000 系列示波器使用的系统,用于在屏幕上以数字和字母形式显示设置(每格的伏特和微秒)。在现代示波器中,屏幕是计算机显示器,能够显示任何文本。但 7000 系列仍然是模拟的,带有一个阴极射线管,电子束在水平和垂直方向上偏转以绘制波形。吉尔伯特设计了一组(模拟!)芯片,可以生成信号来控制电子束在屏幕上绘制数字和字母 [9]。在当时(1970年左右),这是一个巨大的奢侈!

过时与否?
Jones 和 Gilbert 的设计都可以追溯到 20 世纪 60 年代,而 MC1496、NE/SA602/612、SO42P 等混频器芯片则设计于 1970 年代。显然,这样的混频器芯片的需求已经不多了。这是有道理的,因为现在人们不再将单个混频器而是将整个接收器放入芯片中,和/或信号处理很大程度上以数字方式完成。SO42P 的生产早已停产。NXP(原 Philips/Signetics)是 NE602 及其兄弟产品的唯一制造商,并决定今年停止生产。它们会在一段时间内随处可见,但到了某个时候,库存就会耗尽。
四象限乘法器 AD534 于 1977 年推向市场。2006 年,它已在伦敦科学博物馆的“过时模拟计算技术”展览中展出[11]。但这还为时过早,因为截至 2023 年该芯片仍在生产。显然,这种芯片仍然有需求,但它们比之前提到的混频器贵得多。
我还没有真正找到 NE602 的良好替代品。人们很快就会想到古老的 MC1496,它仍在制造中,但不太容易使用:它需要更高的电源电压和外部直流偏置,并且没有内置振荡器。或者,现代芯片适用于 GHz 范围内的频率,通常采用业余爱好者不友好的小型 SMD 封装,并且同样没有内置振荡器。

参考
[1] NE/SA602A 数据表,Philips,1990。
[2] MC1496 数据表,ON Semiconductor,2006。
[3] Howard E. Jones:利用晶体管差分放大器的双输出同步检测器;美国专利 3241078A(1963 年注册)。
[4] Barrie Gilbert:具有亚纳秒响应的精确四象限乘法器,IEEE 固态电路杂志,1968 年 12 月。重印于 [7]。
[5] 巴里·吉尔伯特:天才的齿轮,见[7]。
[6] Thomas H. Lee:连续体的故事:模拟电路的二次采样历史,参见 [7]。
[7] IEEE SSCS 新闻,2007 年秋季。https
https://sscs.ieee.org/images/files/newsletter_archive/sscs_newsletter_200710.pdf
[8] Barrie Gilbert:跨线性电路,历史概述。模拟集成电路和信号处理,1996 年。
[9] Barrie Gilbert:用于字符生成的单片模拟只读存储器,IEEE 固态电路杂志,1971 年 2 月。
[10] https://www.nxp.com/ pcn/202208013DN
[11] James M. Bryant:数字时代的模拟计算。2006。https https://www.analog.com/media/en/analog-dialogue/raqs/computation.pdf
 闽ICP备2021006864号-7
闽ICP备2021006864号-7
 闽公网安备35020602002794号
互联网举报中心
闽公网安备35020602002794号
互联网举报中心